Nombres complexes - Introduction, forme algébrique, opérations de base et représentation géométrique

Introduction générale aux nombres complexes

Les nombres complexes sont apparus au XVIe siècle, notamment dans le cadre de la résolution des équations polynomiales cubiques. Face à des expressions impliquant la racine carrée de nombres négatifs, qui n’ont pas de sens dans l’ensemble des nombres réels, les mathématicien·nes ont été amené·es à étendre le système numérique pour inclure ces nouveaux objets, les nombres complexes.

Aujourd’hui, les nombres complexes sont essentiels dans de nombreux domaines des mathématiques, de la physique et de l’ingénierie. Cette fiche présente une introduction aux nombres complexes, leur forme algébrique, les opérations de base, ainsi que leur représentation géométrique.

1. Origine historique : les équations cubiques et la méthode de Cardan

1.1 Résolution des équations cubiques

L’étude des équations cubiques, c’est-à-dire des polynômes de degré 3, a été le moteur historique de la découverte des nombres complexes. La méthode de résolution dite de Cardan repose sur la substitution :

[ x = u + v, ]

qui permet de transformer l’équation cubique en un système sur [Formule] et [Formule].

Exemple 1 : Résolution de l’équation

[ x^{3} - 6x - 9 = 0. ]

En posant [Formule], on développe :

[ (u+v)^3 - 6(u+v) - 9 = 0, ]

ce qui donne :

[ u^3 + v^3 + 3uv(u+v) - 6(u+v) - 9 = 0. ]

En imposant la condition :

[ 3uv - 6 = 0 \quad \Longleftrightarrow \quad uv = 2, ]

l’équation se simplifie en :

[ u^3 + v^3 = 9. ]

On obtient alors le système :

[ [Contenu mathématique] ]

Ainsi, [Formule] et [Formule] sont racines du polynôme :

[ X^2 - 9X + 8 = 0, ]

dont les racines sont [Formule] et [Formule]. On en déduit :

[ u = \sqrt[3]{1} = 1, \quad v = \sqrt[3]{8} = 2, ]

et donc la solution de l’équation est :

[ x = u + v = 3. ]

1.2 Méthode générale de Cardan

Pour une équation cubique générale :

[ x^{3} + p x + q = 0, ]

on pose [Formule] avec la condition :

[ 3 u v + p = 0. ]

Alors, [Formule] et [Formule] satisfont le système :

[ [Contenu mathématique] ]

Ainsi, [Formule] et [Formule] sont racines du polynôme :

[ X^2 + q X - \frac{p^3}{27} = 0. ]

• Si le discriminant de ce polynôme est positif, la méthode fournit des solutions réelles :

[ u = \sqrt[3]{-\frac{q}{2} + \sqrt{\left(\frac{q}{2}\right)^2 + \left(\frac{p}{3}\right)^3}}, \quad v = \sqrt[3]{-\frac{q}{2} - \sqrt{\left(\frac{q}{2}\right)^2 + \left(\frac{p}{3}\right)^3}}. ]

• Si le discriminant est strictement négatif, il n’y a pas de solutions réelles pour [Formule] et [Formule], ce qui rend la méthode incomplète dans ce cas.

1.3 Limites et extension par Bombelli

Les cas où le discriminant est négatif sont appelés cas irréductibles. Pourtant, toute équation cubique admet au moins une solution réelle, comme l’indique le théorème des valeurs intermédiaires :

[ \lim_{x \to +\infty} x^3 + p x + q = +\infty, \quad \lim_{x \to -\infty} x^3 + p x + q = -\infty, ]

donc la fonction s’annule au moins une fois sur [Formule].

Pour résoudre ces cas, Raphaël Bombelli a accepté d’utiliser la racine carrée de nombres négatifs, introduisant ainsi les nombres complexes.

Exemple 2 : Équation

[ x^{3} = 15 x + 4, ]

soit sous la forme [Formule] avec :

[ p = -15, \quad q = -4. ]

Le polynôme associé pour [Formule] et [Formule] est :

[ X^2 - 4 X + 125 = 0, ]

dont le discriminant est négatif :

[ \Delta = (-4)^2 - 4 \times 1 \times 125 = 16 - 500 = -484 < 0. ]

Bombelli utilise alors :

[ \sqrt{-484} = 22 i, ]

avec [Formule], une nouvelle unité imaginaire.

Les racines sont :

[ 2 + 11 i, \quad 2 - 11 i, ]

et il cherche [Formule] et [Formule] tels que :

[ u^3 = 2 + 11 i, \quad v^3 = 2 - 11 i. ]

Il remarque que :

[ u = 2 + i, \quad v = 2 - i, ]

car :

[ (2 + i)^3 = 2 + 11 i, \quad (2 - i)^3 = 2 - 11 i. ]

La solution réelle est alors :

[ x = u + v = 4. ]

1.4 Schéma résumé : méthode de Cardan et extension par Bombelli

[Diagramme]

2. Définition et forme algébrique des nombres complexes

2.1 L’unité imaginaire [Formule]

Pour formaliser l’usage des racines carrées de nombres négatifs, on introduit une nouvelle unité imaginaire [Formule] définie par :

[ i^2 = -1. ]

Cette définition évite les erreurs liées à la manipulation abusive de la notation [Formule] pour des nombres négatifs.

2.2 Définition axiomatique

Théorème 2.2.1

Il existe un ensemble [Formule], appelé ensemble des nombres complexes, muni de deux opérations (addition et multiplication) qui :

• Prolongent celles des nombres réels,
• Sont associatives, commutatives, distributives,
• Forment un corps (permettant addition, soustraction, multiplication et division sauf par zéro),
• Contiennent un élément [Formule] tel que :

[ i^2 = -1. ]

Tout nombre complexe [Formule] s’écrit de manière unique sous la forme :

[ z = a + i b, \quad a,b \in \mathbb{R}. ]

2.3 Forme algébrique, parties réelle et imaginaire

Définition 2.3.1

Pour [Formule] :

• La forme algébrique est [Formule].
• La partie réelle est [Formule].
• La partie imaginaire est [Formule] (un réel).
• Les nombres de la forme [Formule] (avec [Formule]) sont appelés nombres imaginaires purs.

Remarque : La partie imaginaire est un réel, pas un nombre complexe. Par exemple, pour [Formule] :

[ \mathfrak{Re}(z) = 2, \quad \mathfrak{Im}(z) = -3. ]

Proposition 2.3.2 : Unicité de la forme algébrique

Si deux écritures sont égales :

[ a + i b = a' + i b', ]

alors :

[ a = a', \quad b = b'. ]

3. Opérations de base sur les nombres complexes

3.1 Addition

L’addition de deux nombres complexes se fait en additionnant séparément leurs parties réelles et imaginaires :

[ (a + i b) + (a' + i b') = (a + a') + i (b + b'). ]

Exemple :

[ (2 + 3i) + (4 - 5i) = (2 + 4) + i (3 - 5) = 6 - 2i. ]

3.2 Multiplication par un réel

La multiplication d’un nombre complexe par un réel [Formule] est distributive :

[ \lambda (a + i b) = \lambda a + i (\lambda b). ]

Exemple :

[ -4 \times (2 - 3i) = -8 + 12 i. ]

3.3 Propriétés sur les parties réelle et imaginaire

Pour tous [Formule] et [Formule] :

• [Formule],
• [Formule],
• [Formule],
• [Formule].

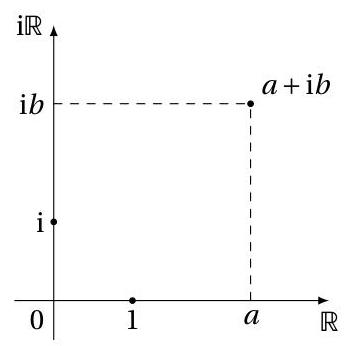
4. Représentation géométrique : le plan complexe

4.1 Le plan complexe

Chaque nombre complexe [Formule] correspond à un point [Formule] de coordonnées [Formule] dans un plan muni d’un repère orthonormé :

• L’axe horizontal (abscisses) représente la partie réelle,
• L’axe vertical (ordonnées) représente la partie imaginaire.

Les nombres imaginaires purs correspondent à la droite verticale, les nombres réels à la droite horizontale.

Définition 4.1.1

• Le point [Formule] est appelé image de [Formule].
• Le nombre [Formule] est appelé affixe du point [Formule].
• Le plan ainsi muni est appelé plan complexe.
• L’axe horizontal est l’axe des réels.
• L’axe vertical est l’axe des imaginaires purs.

4.2 Synthèse des concepts clés

[Diagramme]

Conclusion : points clés à retenir

• Les nombres complexes sont une extension des nombres réels, introduisant une unité imaginaire [Formule] telle que [Formule].
• Chaque nombre complexe s’écrit de manière unique sous la forme algébrique [Formule], où [Formule] est la partie réelle et [Formule] la partie imaginaire réelle.
• Les opérations d’addition et de multiplication par un réel se font en traitant séparément les parties réelle et imaginaire.
• Géométriquement, les nombres complexes sont représentés par des points dans le plan complexe, avec la partie réelle sur l’axe horizontal et la partie imaginaire sur l’axe vertical.
• Historiquement, les nombres complexes sont nés de la nécessité de résoudre les cas irréductibles des équations cubiques, grâce à l’extension de la méthode de Cardan par Bombelli.

Cette double perspective algébrique et géométrique est fondamentale pour la compréhension et la manipulation des nombres complexes dans de nombreux domaines mathématiques et appliqués.

Références

• Méthode de résolution des équations cubiques : Wikipédia - Cubic formula
• Introduction aux nombres complexes : travaux de Bombelli, Descartes et Euler.

Cette fiche synthétise les fondements historiques et mathématiques des nombres complexes, leur forme algébrique, leurs opérations de base, ainsi que leur représentation géométrique dans le plan complexe.