Raccourcis calcul et conditions minimales Tage Mage
Funciones avanzadas disponibles en la aplicación
- Imágenes
- Fórmulas matemáticas
- Diagramas con renderizado profesional y académico en la app
Raccourcis calcul et conditions minimales Tage Mage
Géométrie : Triangles et Cercles
1. Triangle équilatéral
Définition
Un triangle équilatéral est un triangle dont les trois côtés sont égaux. Par conséquent, il est aussi équiangulaire, ce qui signifie que ses trois angles internes valent chacun [Formule].
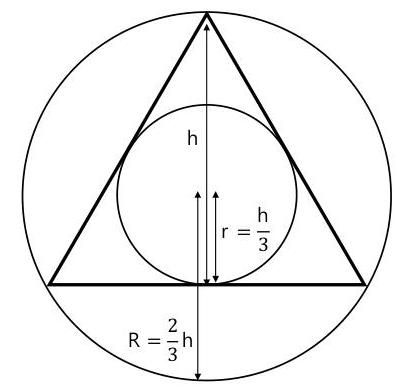
Propriétés principales
| Propriété | Formule |
|---|---|
| Côté | [Formule] |
| Périmètre | [Formule] |
| Aire | [Formule] |
| Hauteur | [Formule] |
| Rayon du cercle circonscrit | [Formule] |
| Rayon du cercle inscrit | [Formule] |
2. Triangles classiques : Triangle rectangle et théorème de Pythagore
Théorème de Pythagore
Dans un triangle rectangle [Formule], où l'angle droit est en [Formule], la relation suivante est toujours vérifiée :
[Formule mathématique]
Cela implique que la longueur de l'hypoténuse [Formule] est toujours supérieure à celle de chacun des deux autres côtés.
Triangles rectangles standards à connaître
-
Triangle 3-4-5
C'est un triangle rectangle classique souvent rencontré dans les exercices du Tage Mage. Si un côté mesure 3, 4 ou 5, on peut rapidement compléter les deux autres côtés en utilisant cette triple triplet. Le côté 5 est toujours l'hypoténuse. -
Multiples du triangle 3-4-5
Les triangles [Formule] et [Formule] sont simplement des multiples de ce triangle de base. -
Triangle 5-12-13
Ce triangle rectangle est moins fréquent. Ici, le côté longueur 5 n'est pas l'hypoténuse (qui est 13).
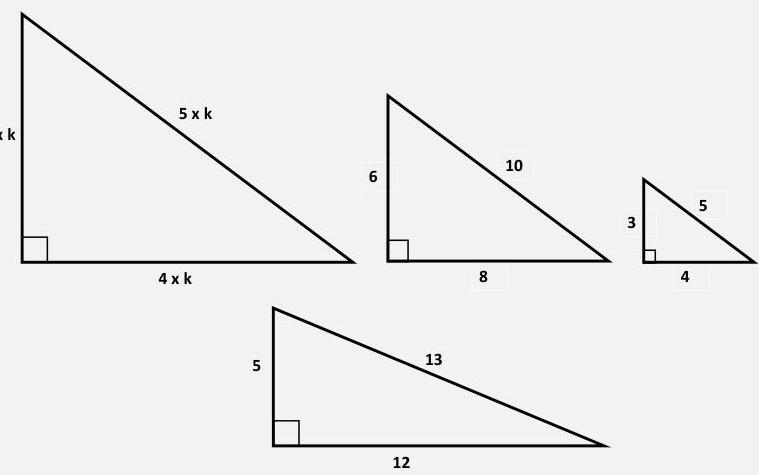
Remarque importante
Tous les triangles vérifiant la relation [Formule] existent, que leurs côtés soient entiers ou non. Cependant, dans les exercices du Tage Mage, on rencontre rarement des triangles avec des longueurs impliquant des racines carrées. Si dans les propositions de réponse, il n'y a pas de racines, il s'agit probablement d'un triangle rectangle classique (dont les côtés sont des entiers comme dans les exemples ci-dessus).
3. Cercles : propriétés et formules essentielles
| Propriété | Formule |
|---|---|
| Rayon | [Formule] |
| Diamètre | [Formule] |
| Périmètre (circumférence) | [Formule] |
| Surface (aire) | [Formule] |
| Longueur d'un arc d'angle [Formule] | [Formule] |
| Surface d'un secteur circulaire d'angle [Formule] | [Formule] |
4. Figures classiques : périmètres et surfaces
| Figure | Paramètres | Périmètre | Surface |
|---|---|---|---|
| Carré | Côté [Formule] | [Formule] | [Formule] |
| Rectangle | Largeur [Formule], Longueur [Formule] | [Formule] | [Formule] |
| Cercle | Rayon [Formule] | [Formule] | [Formule] |
| Losange | Grande diagonale [Formule], Petite diagonale [Formule], Côté [Formule] | [Formule] | [Formule] |
| Triangle | Base [Formule], Hauteur [Formule] | Somme des côtés | [Formule] |
| Parallélogramme | Base [Formule], Hauteur [Formule] | Somme des côtés | [Formule] |
| Trapèze | Grande base [Formule], Petite base [Formule], Hauteur [Formule] | Somme des côtés | [Formule] |
5. Méthode LSV : Relation entre tailles, surfaces et volumes
Cette règle permet d'évaluer rapidement l’effet d’un agrandissement ou d’une réduction sur les dimensions, les périmètres, les surfaces et les volumes.
Passage d’une figure petite à une figure grande par un facteur [Formule]
- Longueurs : se multiplient par [Formule]
- Surfaces : se multiplient par [Formule]
- Volumes : se multiplient par [Formule]
Exemple 1 : Figures planes
Considérons deux figures semblables, l’une petite, l’autre obtenue en multipliant toutes ses dimensions par 3.
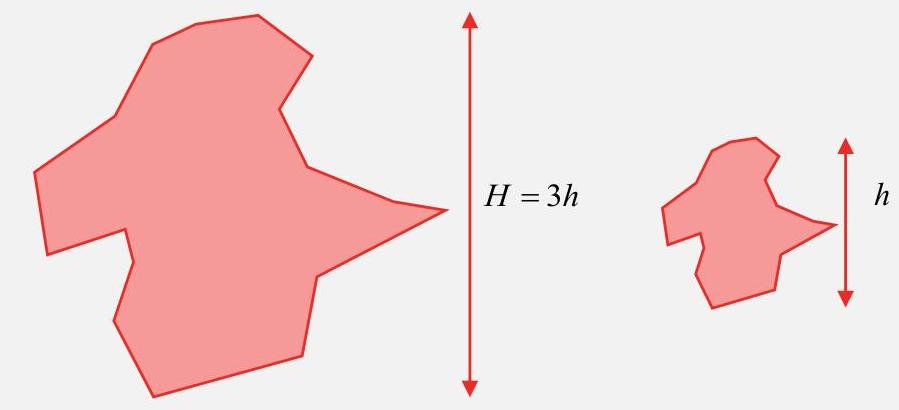
- Les périmètres sont multipliés par 3.
- Les aires sont multipliées par [Formule].
Exemple 2 : Volumes
Si on double chaque côté d’un cube, le volume du grand cube est multiplié par [Formule] par rapport au petit cube.
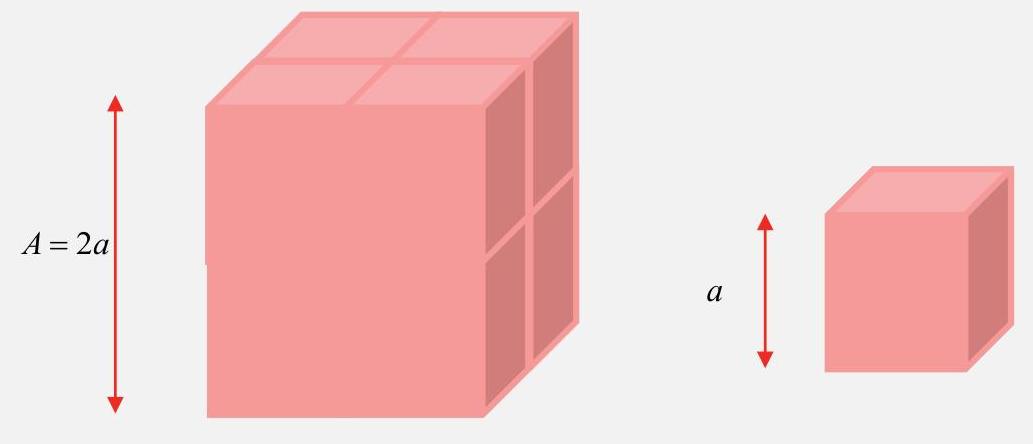
Synthèse rapide
| Type de grandeur | Multiplicateur pour un facteur d’agrandissement [Formule] |
|---|---|
| Longueurs | [Formule] |
| Périmètres | [Formule] |
| Surfaces (aires) | [Formule] |
| Volumes | [Formule] |
Cette fiche regroupe les formules clés et méthodes indispensables pour gérer rapidement les calculs géométriques dans le contexte du Tage Mage, avec un focus sur les triangles classiques, cercles, figures usuelles et la méthode LSV permettant de calculer facilement l’impact des changements d’échelle.
